How to Add Improper Fractions With Different Denominators
Fractions
24 Add and Subtract Fractions with Different Denominators
Learning Objectives
By the end of this section, you will be able to:
- Find the least common denominator (LCD)
- Convert fractions to equivalent fractions with the LCD
- Add and subtract fractions with different denominators
- Identify and use fraction operations
- Use the order of operations to simplify complex fractions
- Evaluate variable expressions with fractions
Before you get started, take this readiness quiz.
- Find two fractions equivalent to
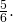
If you missed this problem, review (Figure). - Simplify:
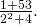
If you missed this problem, review (Figure).
Find the Least Common Denominator
In the previous section, we explained how to add and subtract fractions with a common denominator. But how can we add and subtract fractions with unlike denominators?
Let's think about coins again. Can you add one quarter and one dime? You could say there are two coins, but that's not very useful. To find the total value of one quarter plus one dime, you change them to the same kind of unit—cents. One quarter equals ![]() cents and one dime equals
cents and one dime equals ![]() cents, so the sum is
cents, so the sum is ![]() cents. See (Figure).
cents. See (Figure).
Together, a quarter and a dime are worth ![]() cents, or
cents, or ![]() of a dollar.
of a dollar.

Similarly, when we add fractions with different denominators we have to convert them to equivalent fractions with a common denominator. With the coins, when we convert to cents, the denominator is ![]() Since there are
Since there are ![]() cents in one dollar,
cents in one dollar, ![]() cents is
cents is ![]() and
and ![]() cents is
cents is ![]() So we add
So we add ![]() to get
to get ![]() which is
which is ![]() cents.
cents.
You have practiced adding and subtracting fractions with common denominators. Now let's see what you need to do with fractions that have different denominators.
First, we will use fraction tiles to model finding the common denominator of ![]() and
and ![]()
We'll start with one ![]() tile and
tile and ![]() tile. We want to find a common fraction tile that we can use to match both
tile. We want to find a common fraction tile that we can use to match both ![]() and
and ![]() exactly.
exactly.
If we try the ![]() pieces,
pieces, ![]() of them exactly match the
of them exactly match the ![]() piece, but they do not exactly match the
piece, but they do not exactly match the ![]() piece.
piece.

If we try the ![]() pieces, they do not exactly cover the
pieces, they do not exactly cover the ![]() piece or the
piece or the ![]() piece.
piece.

If we try the ![]() pieces, we see that exactly
pieces, we see that exactly ![]() of them cover the
of them cover the ![]() piece, and exactly
piece, and exactly ![]() of them cover the
of them cover the ![]() piece.
piece.

If we were to try the ![]() pieces, they would also work.
pieces, they would also work.

Even smaller tiles, such as ![]() and
and ![]() would also exactly cover the
would also exactly cover the ![]() piece and the
piece and the ![]() piece.
piece.
The denominator of the largest piece that covers both fractions is the least common denominator (LCD) of the two fractions. So, the least common denominator of ![]() and
and ![]() is
is ![]()
Notice that all of the tiles that cover ![]() and
and ![]() have something in common: Their denominators are common multiples of
have something in common: Their denominators are common multiples of ![]() and
and ![]() the denominators of
the denominators of ![]() and
and ![]() The least common multiple (LCM) of the denominators is
The least common multiple (LCM) of the denominators is ![]() and so we say that
and so we say that ![]() is the least common denominator (LCD) of the fractions
is the least common denominator (LCD) of the fractions ![]() and
and ![]()
Doing the Manipulative Mathematics activity "Finding the Least Common Denominator" will help you develop a better understanding of the LCD.
Least Common Denominator
The least common denominator (LCD) of two fractions is the least common multiple (LCM) of their denominators.
To find the LCD of two fractions, we will find the LCM of their denominators. We follow the procedure we used earlier to find the LCM of two numbers. We only use the denominators of the fractions, not the numerators, when finding the LCD.
Find the LCD for the fractions ![]() and
and ![]()
Find the least common denominator for the fractions: ![]() and
and ![]()
60
Find the least common denominator for the fractions: ![]() and
and ![]()
15
To find the LCD of two fractions, find the LCM of their denominators. Notice how the steps shown below are similar to the steps we took to find the LCM.
Find the least common denominator (LCD) of two fractions.
- Factor each denominator into its primes.
- List the primes, matching primes in columns when possible.
- Bring down the columns.
- Multiply the factors. The product is the LCM of the denominators.
- The LCM of the denominators is the LCD of the fractions.
Find the least common denominator for the fractions ![]() and
and ![]()
Solution
To find the LCD, we find the LCM of the denominators.
Find the LCM of ![]() and
and ![]()
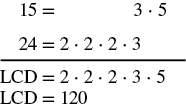
The LCM of ![]() and
and ![]() is
is ![]() So, the LCD of
So, the LCD of ![]() and
and ![]() is
is ![]()
Find the least common denominator for the fractions: ![]() and
and ![]()
96
Find the least common denominator for the fractions: ![]() and
and ![]()
224
Convert Fractions to Equivalent Fractions with the LCD
Earlier, we used fraction tiles to see that the LCD of ![]() is
is ![]() We saw that three
We saw that three ![]() pieces exactly covered
pieces exactly covered ![]() and two
and two ![]() pieces exactly covered
pieces exactly covered ![]() so
so
![]()
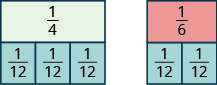
We say that ![]() are equivalent fractions and also that
are equivalent fractions and also that ![]() are equivalent fractions.
are equivalent fractions.
We can use the Equivalent Fractions Property to algebraically change a fraction to an equivalent one. Remember, two fractions are equivalent if they have the same value. The Equivalent Fractions Property is repeated below for reference.
Equivalent Fractions Property
If ![]() are whole numbers where
are whole numbers where ![]()
![]()
To add or subtract fractions with different denominators, we will first have to convert each fraction to an equivalent fraction with the LCD. Let's see how to change ![]() to equivalent fractions with denominator
to equivalent fractions with denominator ![]() without using models.
without using models.
Convert ![]() to equivalent fractions with denominator
to equivalent fractions with denominator ![]() their LCD.
their LCD.
Change to equivalent fractions with the LCD:
![]() and
and ![]()
![]()
Change to equivalent fractions with the LCD:
![]() and
and ![]()
![]()
Convert two fractions to equivalent fractions with their LCD as the common denominator.
- Find the LCD.
- For each fraction, determine the number needed to multiply the denominator to get the LCD.
- Use the Equivalent Fractions Property to multiply both the numerator and denominator by the number you found in Step 2.
- Simplify the numerator and denominator.
Change to equivalent fractions with the LCD:
![]() and
and ![]() LCD
LCD ![]()
![]()
Change to equivalent fractions with the LCD:
![]() and
and ![]() LCD
LCD ![]()
![]()
Add and Subtract Fractions with Different Denominators
Once we have converted two fractions to equivalent forms with common denominators, we can add or subtract them by adding or subtracting the numerators.
Add or subtract fractions with different denominators.
- Find the LCD.
- Convert each fraction to an equivalent form with the LCD as the denominator.
- Add or subtract the fractions.
- Write the result in simplified form.
Add: ![]()
Add: ![]()
![]()
Add: ![]()
![]()
Subtract: ![]()
Simplify: ![]()
![]()
Simplify: ![]()
![]()
Add: ![]()
Add: ![]()
![]()
Add: ![]()
![]()
When we use the Equivalent Fractions Property, there is a quick way to find the number you need to multiply by to get the LCD. Write the factors of the denominators and the LCD just as you did to find the LCD. The "missing" factors of each denominator are the numbers you need.

The LCD, ![]() has
has ![]() factors of
factors of ![]() and
and ![]() factors of
factors of ![]()
Twelve has two factors of ![]() but only one of
but only one of ![]() —so it is 'missing' one
—so it is 'missing' one ![]() We multiplied the numerator and denominator of
We multiplied the numerator and denominator of ![]() by
by ![]() to get an equivalent fraction with denominator
to get an equivalent fraction with denominator ![]()
Eighteen is missing one factor of ![]() —so you multiply the numerator and denominator
—so you multiply the numerator and denominator ![]() by
by ![]() to get an equivalent fraction with denominator
to get an equivalent fraction with denominator ![]() We will apply this method as we subtract the fractions in the next example.
We will apply this method as we subtract the fractions in the next example.
Subtract: ![]()
Subtract: ![]()
![]()
Subtract: ![]()
![]()
Add: ![]()
Add: ![]()
![]()
Add: ![]()
![]()
In the next example, one of the fractions has a variable in its numerator. We follow the same steps as when both numerators are numbers.
Add: ![]()
Add: ![]()
![]()
Add: ![]()
![]()
Identify and Use Fraction Operations
By now in this chapter, you have practiced multiplying, dividing, adding, and subtracting fractions. The following table summarizes these four fraction operations. Remember: You need a common denominator to add or subtract fractions, but not to multiply or divide fractions
Summary of Fraction Operations
Fraction multiplication: Multiply the numerators and multiply the denominators.
![]()
Fraction division: Multiply the first fraction by the reciprocal of the second.
![]()
Fraction addition: Add the numerators and place the sum over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
![]()
Fraction subtraction: Subtract the numerators and place the difference over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
![]()
Simplify:
- ⓐ
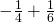
- ⓑ
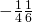
Solution
First we ask ourselves, "What is the operation?"
ⓐThe operation is addition.
Do the fractions have a common denominator? No.
| | |
Find the LCD. 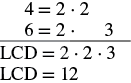 | |
| Rewrite each fraction as an equivalent fraction with the LCD. | 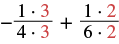 |
| Simplify the numerators and denominators. | |
| Add the numerators and place the sum over the common denominator. | |
| Check to see if the answer can be simplified. It cannot. |
ⓑThe operation is division. We do not need a common denominator.
| | |
| To divide fractions, multiply the first fraction by the reciprocal of the second. | |
| Multiply. | |
| Simplify. | |
Simplify each expression:
- ⓐ
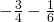
- ⓑ
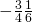
Simplify each expression:
- ⓐ
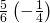
- ⓑ
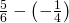
Simplify:
- ⓐ
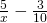
- ⓑ
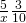
Simplify:
- ⓐ
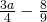
- ⓑ
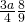
Simplify:
- ⓐ
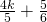
- ⓑ
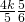
Use the Order of Operations to Simplify Complex Fractions
In Multiply and Divide Mixed Numbers and Complex Fractions, we saw that a complex fraction is a fraction in which the numerator or denominator contains a fraction. We simplified complex fractions by rewriting them as division problems. For example,
![]()
Now we will look at complex fractions in which the numerator or denominator can be simplified. To follow the order of operations, we simplify the numerator and denominator separately first. Then we divide the numerator by the denominator.
Simplify complex fractions.
- Simplify the numerator.
- Simplify the denominator.
- Divide the numerator by the denominator.
- Simplify if possible.
Simplify: ![]()
Simplify: ![]() .
.
![]()
Simplify: ![]() .
.
272
Simplify: ![]()
Simplify: ![]() .
.
2
Simplify: ![]() .
.
![]()
Evaluate Variable Expressions with Fractions
We have evaluated expressions before, but now we can also evaluate expressions with fractions. Remember, to evaluate an expression, we substitute the value of the variable into the expression and then simplify.
Evaluate ![]() when
when ![]()
Key Concepts
- Find the least common denominator (LCD) of two fractions.
- Factor each denominator into its primes.
- List the primes, matching primes in columns when possible.
- Bring down the columns.
- Multiply the factors. The product is the LCM of the denominators.
- The LCM of the denominators is the LCD of the fractions.
- Equivalent Fractions Property
- Convert two fractions to equivalent fractions with their LCD as the common denominator.
- Find the LCD.
- For each fraction, determine the number needed to multiply the denominator to get the LCD.
- Use the Equivalent Fractions Property to multiply the numerator and denominator by the number from Step 2.
- Simplify the numerator and denominator.
- Add or subtract fractions with different denominators.
- Find the LCD.
- Convert each fraction to an equivalent form with the LCD as the denominator.
- Add or subtract the fractions.
- Write the result in simplified form.
- Summary of Fraction Operations
- Fraction multiplication: Multiply the numerators and multiply the denominators.
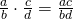
- Fraction division: Multiply the first fraction by the reciprocal of the second.
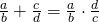
- Fraction addition: Add the numerators and place the sum over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
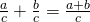
- Fraction subtraction: Subtract the numerators and place the difference over the common denominator. If the fractions have different denominators, first convert them to equivalent forms with the LCD.
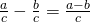
- Fraction multiplication: Multiply the numerators and multiply the denominators.
- Simplify complex fractions.
- Simplify the numerator.
- Simplify the denominator.
- Divide the numerator by the denominator.
- Simplify if possible.
Practice Makes Perfect
Find the Least Common Denominator (LCD)
In the following exercises, find the least common denominator (LCD) for each set of fractions.
![]()
![]()
20
![]()
![]()
48
![]()
![]()
240
![]()
![]()
245
![]()
![]()
60
Convert Fractions to Equivalent Fractions with the LCD
In the following exercises, convert to equivalent fractions using the LCD.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Add and Subtract Fractions with Different Denominators
In the following exercises, add or subtract. Write the result in simplified form.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Identify and Use Fraction Operations
In the following exercises, perform the indicated operations. Write your answers in simplified form.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Use the Order of Operations to Simplify Complex Fractions
In the following exercises, simplify.
![]()
![]()
![]()
![]()
![]()
32
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Mixed Practice
In the following exercises, simplify.
![]()
![]()
![]()
![]()
![]()
−9
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
1
![]()
![]()
![]()
In the following exercises, evaluate the given expression. Express your answers in simplified form, using improper fractions if necessary.
![]() when
when ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
−2
![]()
![]()
3
Everyday Math
Decorating Laronda is making covers for the throw pillows on her sofa. For each pillow cover, she needs ![]() yard of print fabric and
yard of print fabric and ![]() yard of solid fabric. What is the total amount of fabric Laronda needs for each pillow cover?
yard of solid fabric. What is the total amount of fabric Laronda needs for each pillow cover?
Baking Vanessa is baking chocolate chip cookies and oatmeal cookies. She needs ![]() cups of sugar for the chocolate chip cookies, and
cups of sugar for the chocolate chip cookies, and ![]() cups for the oatmeal cookies How much sugar does she need altogether?
cups for the oatmeal cookies How much sugar does she need altogether?
![]()
Writing Exercises
Explain why it is necessary to have a common denominator to add or subtract fractions.
Explain how to find the LCD of two fractions.
Answers will vary.
Self Check
ⓐ After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
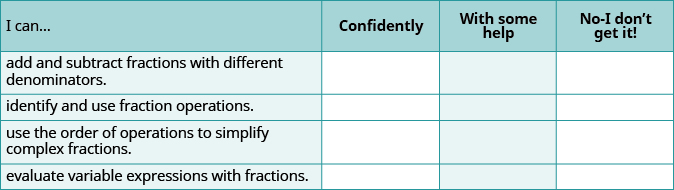
ⓑ After looking at the checklist, do you think you are well prepared for the next section? Why or why not?
Glossary
- least common denominator (LCD)
- The least common denominator (LCD) of two fractions is the least common multiple (LCM) of their denominators.
How to Add Improper Fractions With Different Denominators
Source: https://opentextbc.ca/prealgebraopenstax/chapter/add-and-subtract-fractions-with-different-denominators/
0 Response to "How to Add Improper Fractions With Different Denominators"
Post a Comment